Команда исследователей из Будапешта показала, как теоретические концепции математики обретают реальную жизнь. Они обнаружили совершенно новую форму «мягкой ячейки», которая перешла от математической возможности к обилию природных примеров. Источник: Popular Mechanics.
Математики издавна увлекались изучением форм. Используя острые края и множество точек, они посвятили столетия тому, чтобы увидеть, как эти формы сочетаются друг с другом, обеспечивая бесконечные возможности укладки плитки. Но уравнения, используемые при математическом формообразовании, с их жесткими линиями и острыми краями, как правило, редко пересекаются с природой.
Группа исследователей из Будапештского технологического университета объявила, что они открыли новый естественный класс формы плитки с изогнутыми краями. Свои выводы они загрузили на сервер препринтов arXiv. Этим формам, получившим названия «мягкие ячейки» и «z-ячейки», не хватает характерных углов теоретической математики, но они все равно подходят друг другу как в двух, так и в трех измерениях.
«Центральная проблема геометрии – замощение пространства простыми структурами», – пишут авторы. «Классические решения, такие как треугольники, квадраты и шестиугольники на плоскости, а также кубы и другие многогранники в трехмерном пространстве, построены с острыми углами и плоскими гранями. Однако многие плитки в природе характеризуются формой с изогнутыми краями, неплоскими гранями и небольшим количеством острых углов, если последние вообще имеются. И важный вопрос здесь состоит в том, чтобы связать прототипы острых плиток с более мягкими естественными формами».
Новый класс конструкционной мозаики
Команда венгерских ученых считает, что они решили проблему размерностей при помощи нового «бесконечного класса многогранных мозаик», способных плавно деформироваться в мягкие плитки и создавать мягкие версии ячеек, обычно связанных с точечными решетками как в двух, так и в трех измерениях.
«Эти формы возникают не только в искусстве, но и в биологии», – заявил для New Scientist руководитель исследования Габор Домокос. «Если вы посмотрите на участки мышечной ткани, то увидите, что клетки имеют всего два острых угла, т.е. на один меньше, чем у треугольника и это совершенно особый вид мозаики».
«Примечательно, что эти идеальные мягкие формы, рожденные геометрией, в изобилии встречаются в природе, от клеток до оболочек», – отметил он.
В двух измерениях эти формы мягкой оболочки довольно легко описать – согласно венгерским ученым, они представляют собой «ячейки с изогнутыми границами, имеющими только два угла». В трехмерном пространстве все становится немного сложнее, но цель та же: позволить вещам быть гибкими и свести к минимуму количество присутствующих «углов». В 3D форме мягкие ячейки могут вообще не иметь углов.
«Мы обнаружили, что архитекторы интуитивно находили такие формы, когда хотели избежать углов», – сообщил Домокос.
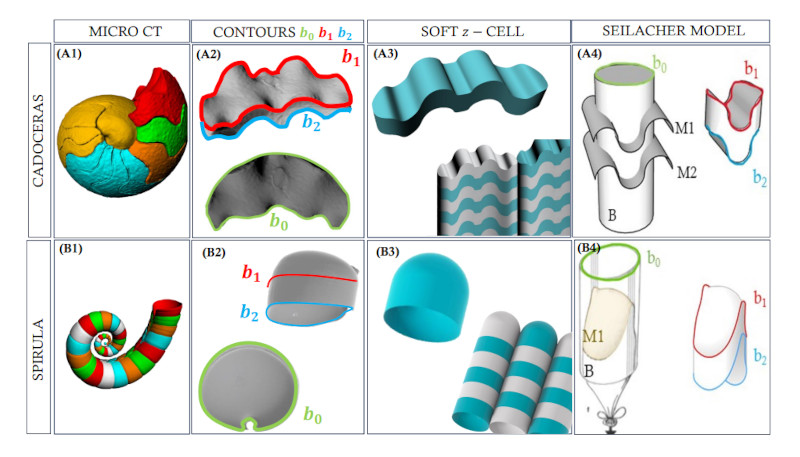
В основной части научной статьи объясняется, как морские ракушки становятся естественным примером этой формы. Как известно, раковина формируется из нескольких камер, и ее рост, по-видимому, происходит по регулируемой схеме. Используя компьютерный томограф, команда исследователей обнаружила, что, когда они измеряли ракушки в трех измерениях, они не могли найти острые углы, хотя двухмерный вид ракушек воспринимается иначе. Это заставило венгерских ученых поверить, что морская ракушка является ярким примером формы мягких ячеек, а также показывает, насколько далеко природа превосходит наше современное понимание геометрии.